Teorema del Coseno

Teorema del Coseno

El teorema del coseno es una generalización del teorema de Pitágoras en los triángulos no rectángulos que se utiliza, normalmente, en trigonometría.

El teorema relaciona un lado de un triángulo con los otros dos y con el coseno del ángulo formado por estos dos lados:

Teorema del coseno Dado un triángulo ABC, siendo α, β, γ, los ángulos, y a, b, c, los lados respectivamente opuestos a estos ángulos entonces:

            a² = b² + c² - 2bc cos a

b² = a² + c² - 2ac cos b

c² = a² + b² - 2ac cos g

En la mayoría de los idiomas, este teorema es conocido con el nombre de teorema del coseno, denominación no obstante relativamente tardía. En francés, sin embargo, lleva el nombre del matemático persa Ghiyath al-Kashi que unificó los resultados de sus predecesores.

Vamos a un ejemplo:

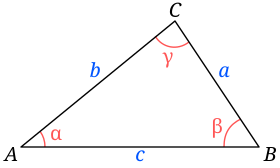
Determinemos la longitud de c en el triángulo ABC de la figura:

c2 = a2 + b2 - 2ab cos g c2 =  c2 = 8 c =

 

Teorema del Seno

Teorema del Seno

En trigonometría, el teorema del seno es una relación de proporcionalidad entre las longitudes de los lados de un triángulo y los senos de los ángulos respectivamente opuestos.

Usualmente se presenta de la siguiente forma:

Teorema del seno Si en un triángulo ABC, las medidas de los lados opuestos a los ángulos A, B y C son respectivamente a, b, c, entonces

Aplicación del Teorema del Seno

El teorema del seno es utilizado para resolver problemas en los que se conocen dos ángulos del triángulo y un lado opuesto a uno de ellos. También se usa cuando conocemos dos lados del triángulo y un ángulo opuesto a uno de ellos. 

Ejemplo:

Tenemos un triángulo en el cual conocemos: A: 30°; B: 100°; c: 5cm. Y debemos calcular las medidas restantes.

Como A + B + C = 180°, C = 180 - 30 -100 = 50°

Para el cálculo de las longitudes utilizamos el teorema del seno:

a = c

sen A sen C

a = c senA = 5 sen30° = 2.5 = 3.26

sen C sen 50° 0.76

y b se calcula igual:

b = c

sen B sen C

b = c senB = 5 sen100° = 4.92 = 6.42

sen C sen 50° 0.76

De tal modo que ya tenemos todos los datos.

Teorema de Pitágoras

Teorema de Pitágoras

El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).

Teorema de Pitágoras En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Pitágoras de Samos

Si un triángulo rectángulo tiene catetos de longitudes  y 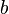, y la medida de la hipotenusa es , se establece que:

Ejemplo:

Calcular la hipotenusa de un triángulo rectángulo si sus catetos mien respectivamente 3.0 m y 5.0 m.

Solución:

Tomemos como base la figura 2.

Ejemplo:

El lado de un cuadrado vale 10.0 m . Calcular el valor de su diagonal

Solución:

La diagonal d del cuadrado corresponde a la hipotenusa del triángulo rectángulo que tiene como catetos dos lados del cuadrado. (figura 3).

Distancia entre dos Puntos

Distancia entre dos puntos

Por haberlo estudiado, sabemos que el Plano cartesiano se usa como un sistema de referencia para localizar puntos en un plano.

Otra de las  utilidades de dominar los conceptos sobre el Plano cartesiano radica en que, a partir de la ubicación de las coordenadas de dos puntos es posible calcular la distancia entre ellos.

Cuando los puntos se encuentran ubicados sobre el eje x (de las abscisas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas (x₂ – x₁) .

Ejemplo:

La distancia entre los puntos (–4, 0) y (5, 0) es 5 – (–4) = 5 +4 = 9 unidades.

Cuando los puntos se encuentran ubicados sobre el eje y (de las ordenadas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas.

Ahora, si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación:

               

Para demostrar esta relación se deben ubicar los puntos 

P₁(x₁, y₁) y P₂(x₂, y₂) en el sistema de coordenadas, luego formar un triángulo rectángulo de hipotenusa P₁P₂ y emplear el Teorema de Pitágoras.

Ejemplo:

Calcula la distancia entre los puntos P₁(7, 5) y P₂(4, 1)

d = 5 unidades

Ecuación General de la Recta

Ecuación General de la Recta

Partiendo de la ecuación continua la recta    

                                   

Y quitando denominadores se obtiene:

                                 

                                  

Trasponiendo términos:

                               

Haciendo 

          

Se obtiene

                                                                   

Esta expresión recibe el nombre de ecuación general o implicita de la recta. De esta forma se acostumbra a dar la respuesta cuando se pide la ecuación de una recta.

Las componentes del vector director son:

                                         

La pendiente de la recta es:

                                           

Hallar: ecuación de la que pasa por A (1,5) y tiene como vector director  igual (-2, 1).

                                       

                                                           

                                      

Hallar la ecuación de la que pasa por A (1,5) y tiene como pendiente m = -2.

                        

                              

                                     

Ecuación de la circunferencia

Ecuación de la Circunferencia

Si el centro de la circunferencia coincide con el origen de coordenadas la ecuación queda reducida a:

                                                

                           

Escribir la ecuación de la circunferencia de centro (3, 4) y radio 2.

                     

                      

                      

Dada la circunferencia de ecuación x² + y² - 2x + 4y - 4 = 0, hallar el centro y el radio.

       

                   

                     

Hallar: ecuación circunferencia que pasa por los puntos A(2,0), B(2,3), C(1, 3).

Si sustituimos x e y en la ecuación  por las coordenadas de los puntos se obtiene el sistema: